
서론
알고리즘 공부를 위한 자료구조의 기본적인 개념을 정리하였습니다.
본론
● 1.1 배열과 연결리스트

- 배열 : 같은 자료형을 갖는 여러 원소를 하나의 변수이름으로 모아놓은 데이터의 집합
😄 인덱스를 통한 직접적인 원소접근 -> 빠르고 동일한 접근시간
논리적 순서와 저장된 물리적 순서 일치, 표현이 간단
😡 삽입/삭제시 추가적인 자료의 이동에 따른 오버헤드 발생가능 (원소의 논리적인 순서와 동일하게 물리적인 순서를 유지하는 상황에서 발생...) , 배열의 크기가 대부분 정적으로 결정되기에 삽입과 삭제가 동적으로 방생하는 상황에서 적절한 배열의 크기를 미리 결정하는 것이 어려워 이로인해 오버플로나 저장공간 낭비 초래
이러한 문제점을 보완한 형태의 자료구조가 연결리스트!!

- 연결리스트 : 데이터필드와 링크필드로 이루어진 노드라는 저장구조를 이용한 녀석
😄 간단한 삽입과 삭제과정, 논리적순서와 물리적 순서 일치시킬 필요 없음
😡 특정 데이터를 접근하기 위해서 첫번째 데이터를 가진 노드부터 시작해서 원하는 데이터가 있는 노드까지 모든 노드를 차례로 방문해야함
● 1.2 스택과 큐
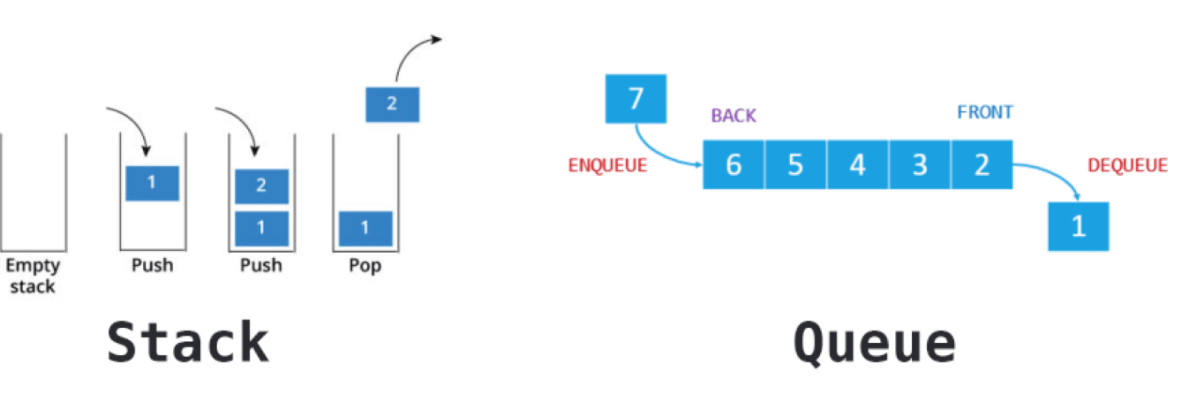
- 스택 : 후입선출 (LIFO) 구조, 리스트의 한쪽 끝에서만 삽입(push)과 삭제(pop)이 나타나는 리스트
- 큐 : 선입선출(FIFO) 구조, 리스트의 한쪽 끝에서는 삽입만 가능하고 다른 한쪽에서는 삭제만 수행되는 리스트
큐의 가장 앞부분 (front, head) 라고 하며 뒷부분을 (rear, tail) 이라고 함
● 1.3 트리
- 트리: 하나 이상의 노드로 구성된 유한 집합 T
트리는 노드라고하는 정보항목이 간선으로 연결되어 계층적 구조를 이루는 비선형 자료구조
⚡️트리의 필수조건
조건 1 : T의 원소 가운데 단 하나의 루트노드가 존재함
조건 2: 루트노드를 제외한 나머지 노드는 n개(n >= 0) 의 서로 분리된 부분집합 T1, T2, T3 ... Tn 으로 나누어지며 각 Ti 를 트리 T의 서브트리라고 한다.

👀 트리의 주요용어
차수(degree) : 노드의 서브트리의 개수를 그 노드의 차수 또는 분기수라고 한다.
리프(leaf)노드 : 차수가 0인 노드를 리프노드 또는 단말노드(terminal node)라고 한다. 단말노드 이외의 나머지 노드는 비단말노드(nonterminal node)라고 함
부모(Parent), 형제(Sibling), 자식(Child) : 어떤 노드 Z의 서브트리들의 루트노드들을 Z의 자식노드라고 하고 Z는 이 자식노드의 부모노드, 동일한 부모를 갖는 노드를 형제노드라 함
조상(ancestor), 후손(descendant) : 부모와 자식의 관계를 좀 더 확장시킨 개념, 한 노드의 조상은 해당노드에서 루트노드까지의 모든 노드를 의미 (EX: N의 조상 : H, D, A) // 반대로 C의 후손은 F, K, L (해당 노드로 부터 경로상에 있는 단말노드까지...)
트리의 차수: 트리내의 노드의 차수중 최대 차수를 의미
레벨: 노드의 레벨이란 루트노드로부터의 거리를 의미
루트 노드 자체의 거리 0, 어떤 노드의 레벨이 l일 때 자식노드의 레벨은 l + 1
높이/깊이 : 트리의 높이 or 깊이는 그 트리에 속하는 노드의 최대레벨에 1을 더한것 레벨이 3인경우 깊이는 4
숲 : 숲이란 n(>=0)개의 분리된 트리의 집합, 트리에서 루트노드를 제거하면 숲이된다. 위 트리Z 에서 A를 제거하면 세개의 트리로 된 숲이 된다.

순서트리
이진트리
● 1.4 그래프
결론
◇ 요약 ◇
①
②
③
④
⑤
참고자료
'■ CS ■ > Algorithm' 카테고리의 다른 글
| #06 정렬알고리즘 (0) | 2021.03.07 |
|---|---|
| #05 욕심쟁이 알고리즘 (0) | 2021.03.07 |
| #04 동적프로그래밍 알고리즘 (0) | 2021.03.07 |
| #03 분할정복 알고리즘 (0) | 2021.03.07 |
| #01 알고리즘 Intro (0) | 2019.11.14 |




댓글